Data Structures and Database Indexes
Alex Woods
June 21, 2019
A database index is an extra data structure in a storage engine w/ the goal of faster retrieval. It’s not the primary storing entity for the data, and it has to be maintained on writes.
Hash Index
The simplest type of index. The keys are whatever column the index is built on, and the value is the location of the data on disk—this prevents us for having to scan for the values.
Hash indexes work well for simple equality (select * from table_name where id = 4;). They don’t work for range queries (select * from table_name where id > 4 and where id < 16;), due to the nature of a hash map (hash functions are by no means sequential).
Hash indexes are stored in memory (in RAM), and so if the database crashes, they’re wiped out and have to be rebuilt.
Note that putting and getting from a hash table is O(1) in most cases (as in, when a hash collision doesn’t occur), so this type of index is extremely fast, and works well for it’s limited set of use cases (equality!). Note that hash collisions are minimized when sufficient memory is allocated to the hashmap.
B-Tree Index
This is the most common type of index. In fact, when you use create index in Postgres, it creates a B-Tree index by default.
B-Trees keep the key-value pairs sorted in order by key, which allows for great performance on range queries.
A B-Tree is made up of pages, with page size P, each of which has b possible references to child pages. We call b the branching factor. If a page has d children, then it is storing d-1 keys, and d <= b.
When dealing with the data structure (as opposed to the database index), you will often hear "pages" referred to as nodes. They’re the same thing, just different contexts.
Maintaining Balance
The key properties of a B-Tree are the following:
- Each node can store b-1 keys, where b is the branching factor. This is in contrast to something like a splay tree, where each node stores only a single value.
- It is always balanced. Insert and delete operations, if they put the tree out of balance, are followed by some balancing operation. (A splay tree acts the same in this regard).
For the following example, we’ll be dealing with 2-4 trees, which are a B-Tree, with a branching factor of 4. Meaning, a node can have a maximum of 4 children, and a maximum of 3 values.
Overflow
When a node overflows (the # of keys allowed has been exceeded upon an insertion), we split the node.
e.g. If a node has keys [1,2,3,4], it has overflowed. Therefore, we must split it.
We do this by promoting one of the keys in the middle to the parent, and making children out of the keys on the left and right of the value promoted.
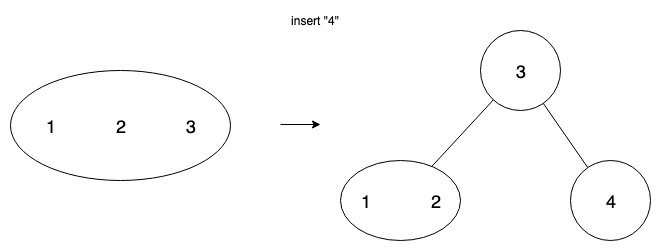
One challenge for implementers is that overflow can propagate—if we overflow a leaf node, then we split it, and promote a key, that can cause overflow on the parent node, which we will then further have to split. This can (and should) be solved recursively, but it is nonetheless a challenge.
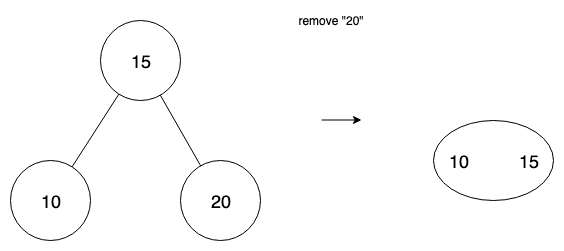
Underflow
Upon deletion of a value, we can have a node that has no values. We have two cases—transfer and fusion. When a node has a sibling node with at least 2 values, then we can perform transfer.
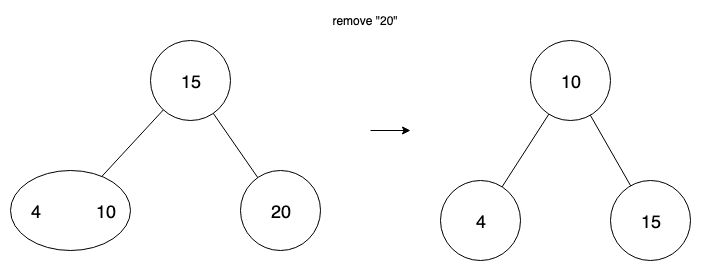
In the case where there isn’t such a sibling, and transferring would just propagate the underflow to the sibling, we use fusion—the combining of two nodes. We combine the empty node with its sibling, and also move a value from parent into that node.
This website has a fantastic visualization of how it works. The main thing to take away about the structure is that it is always balanced, and so when we go to search for a key-value pair, it is worst case O(logn).
Storage Capacity
B-Tree indexes, unlike hashmap indexes, are usually maintained on disk. This is because we usually keep a large page size. When a B-Tree has a large page size and branching factor, it has a very high storage capacity.
storage capacity = (b^n) * P
Where n is the length of the tree, b is the branching factor, and P is the page size. e.g.
500^4 * 4KB = 250TB (example from [1]).